Introduction
What is the "Projektpraktikum"?
The Projektpraktikum is a mandatory course at our faculty in which groups of students have to plan, realise and evalauate own experiments. Our project was carried out at the Max Planck Institute For Dynamics and Self-Organization under the supervision of Prof. Dr. Jürgen Vollmer and Dr. James Clewett. It is entitled Maxwell's Demon in Granular Gases and deals with clustering processes in granular gases. The project report and poster can be downloaded here.
Motivation
The term Granular matter refers to dissipative systems of discrete macroscopic particles. Those systems were not taken into account by physicists for quite a long time but have developed to a subject of vivid interest in the last decades because of their attractively surprising behaviour and its relevance for many issues of everyday life, industrial production and science (e.g. geological processes). [see K. van der Weele. Contemporary Physics, 49(3):157–178, 2008.]
Granular matter can be present in different states that may be reminiscent of gases, liquids, solids or mixtures of these (multiphase flows) but it shows properties that are contra-intuitive at the first glance. For example it may enlarge its volume in response to an external pressure whereas the opposite would be expected for a classical system in thermodynamic equilibrium. [see Jaeger, Nagel, Behringer. Rev. Mod. Phys., 68, 1996.]
Furthermore, granular gases tend to spontaneously form clusters - i.e. they separate into rather dense and dilute regions by itself - while a classical system would develop to a preferably uniform distribution. [see K. van der Weele. Contemporary Physics, 49(3):157–178, 2008.]
Is it possible to violate the second law of thermodynamics with help of a little demon?
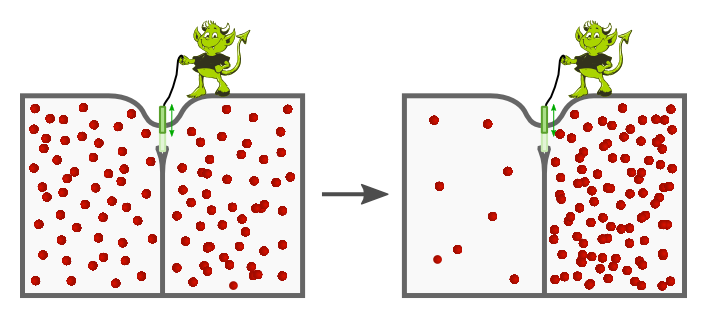
The latter may be reminiscent of a variant of the famous thought experiment published by James Clerk Maxwell in 1872 known as Maxwell's demon: A box divided into two compartments is filled with a homogeneous gas. The compartments are connected by a little trapdoor that - in the ideal case - can be opened and closed without doing work. Now a little demon may control the door in a way that he lets the particles pass only in one direction. By that he induces a pressure gradient which can be used to drive a machine subsequently. This seems to violate the second law of thermodynamics (decrease of entropy).
However, this contradiction was resolved in the 20th century by showing that the demon causes an additional increase of entropy related to the information exchange. [see A. F. R. Harvey Leff. Maxwell’s Demon. 1990.]
Our experiment
We want to analyse a granular system and in particular observe its tendency to spontaneously form regions of high or low concentration. A simple realisation is a perspex box with ping-pong balls (idealised as spherically, uniform particles that dissipate energy under collisions) which are driven by an oscillating bottom plate.

If the box is in addition divided into two compartments of same size by placing a half-height wall in the middle of the box, one is able to compare the particle densities of two different regions of the system. This experiment is based on a set-up that was first suggested by H.J. Schlichting and V. Nordmeier. Here you can find more about the experimental setup.
In addition we want to do a computer simulation of this experiment in order to determine quantities (e.g. velocity distributions) that are rather difficult to access in experiments or to consider more complex settings.
